과제를 해결한 과정을 정리한 글로 부정확하거나 비효율적일 수 있습니다!
YACC란?
Yet Another Compiler Compiler
또 다른 컴파일러 컴파일러라는 뜻이다.
즉 컴파일러를 컴파일해주는 것이란 뜻인데 이게 무슨 말일까?
결론부터 말하자면 구문분석 후 구문에 따른 동작을 지시하기 위한 프로그램이다.
나는 중국식냉면을 먹었다.
라는 문장에서 주어 수식어 목적어 동사를 구별해서 아~ 에벱이 중국식냉면을 먹었구나 하고 이해시켜주기 위한 것이라고 할 수 있다.
그럼 계산기에서 구문분석이란 뭘까?
3+2*(1-4)라는 식을 생각해보자 컴퓨터에게 이 문자들은 그저 하나하나의 문자일뿐 수식의 의미를 가지지 않으며 무엇을 어떠한 순서로 계산해야 할지도 모른다.
다만 우리가 실제로 쓰는 프로그래밍언어에는 이 전자계산기와 같은 구문분석프로그램이 들어가 있어서 인식해줄 뿐이다.
그럼 그 구문분석이 어떻게 이뤄지는지 보도록 하는 것이 이번의 과제였다.
먼저 교수가 제시한 스팩을 확인해보자
- 4칙연산과 ^(거듭제곱)
- 메모리
- log fabs(절대값) exp sqrt cos 함수
- ()와 계산순서
- 정수형끼리의 계산은 정수형 실수형을 포함한 계산은 실수형으로 출력
- 메모리 또한 정수형과 실수형을 구별할것
많다.. 하지만 교수의 PPT를 잘 뒤적거리면 골격이 되는 코드들은 찾을 수 있었기에 그것들을 어떻게 변형시키고 추가시키면 될 것 같았다.
LEX
먼저 lex의 일부인 토큰부분을 보자
위에서 yacc는 구문분석을 위한 프로그램이라고 했는데 정확히는 구문 분석은 lex가 담당한다. 그 분석결과와 구성에 따라 어떻게 해석하고 행동할지가 적혀있는 부분이 yacc라고 할 수 있다.
아래의 lex파일에서는 필요한 요소들에 대해 어떠한 토큰을 yacc에게 반환하라고 지시하고 있다.
ws [ \t]
symbol [=+\-*/\^()[\]\n]
digit [0-9]
other .
%%
{ws}+
{symbol} { return (yytext[0]); }
"M" { return (MEM); }
"exp" { return (EXP); }
"log" { return (LOG); }
"sqrt" { return (SQRT); }
"cos" { return (COS); } /* ADD TOKEN COS, FABS*/
"fabs" { return (FABS); }
{digit}+ { sscanf(yytext, "%d", &yylval.ival);
return (INTC);
}
{digit}+"."{digit}* { sscanf(yytext, "%lf", &yylval.rval);
return (REALC);
}
"(INT)" { return (INT_CAST);} /* ADD TOKEN FOR CAST*/
"(DOUBLE)" { return (DBL_CAST);}
{other} { fprintf(stderr, "Illegal character '%c' ignored\n", yytext[0]);}
{}와 위의 [] 안에 있는 것은 정규표현식에의한 문자의 표현이며 "" 안에 있는것은 일반적인 정확한 일치를 요구하는 표현이다.
정규표현식에대해 길게적지는 않지만 예를들면 digit은 0~9까지의 숫자 {digit}+는 숫자가 1개이상 이어지는 문자열과 같은 의미를 가진다.
교수의 PPT에는 sqrt까지의 토큰의 정의가 있었기에 fabs와 cos에대한 해석을 추가했으며 (INT) (DOUBLE)의 형변환도 인식이 가능하게 토큰을 추가했다.
그 외의 경우 other로 분류되어 에러로 해당 문자를 무시한다고 출력하고 무시한다.
YACC
이제 이 토큰들이 어떠한 문법을 가져야하는지 또 그 문법에 따른 행동이 정의되어있는 yacc파일을 보자
이번 과제의 경우에는 변수형을 정수인지 실수인지를 구별하는 것이 가장 큰 과제였다.
그래서 변수의 구조를 다음과 같이 정의했다.
%union{
int ival;
double rval;
struct {
enum {INT, DBL} Type;
union {
int I;
double D;
} V_fld;
} Val;
}
단순 정수형 ival 단순실수형 rval 이 있고 그 이외에 일반적인 변수는 구조체를 가진다.
이 구조체에는 그 변수의 타입과 V_fld에 실수일 경우 실수 값 정수일 경우에는 정수 값이 저장하도록 한다.
이 구조체를 사용하는 것으로 변수의 형을 기억할 수는 있지만 문제는 단순 연산을 할 수가 없다. X라는변수와 Y라는 변수를 더한다고 생각해보자. 이 경우에는 더하면 구조체끼리의 덧셈이되어 에러가 발생할 것 이다.
이 문제를 해결하며 필요한 연산들을 지원하기 위해 다양한 메크로의 정의가 필요했다.
예를 들면 다음과 같은 기본적인 4칙연산을 위한 매크로가 있다
#define ARITH(R, X, OP, Y) \
if (R.Type == INT && Y.Type == INT) { \
R.Type = INT; \
R.V_fld.I = X.V_fld.I OP Y.V_fld.I; \
} else {\
R.Type = DBL; \
R.V_fld.D = (X.Type==INT ? (double)X.V_fld.I : X.V_fld.D) \
OP (Y.Type==INT ? (double)Y.V_fld.I : Y.V_fld.D); \
}
연산자를 OP 저장할 곳을 R라 지정하여 X OP Y 의 연산을 한다. 예를들면 OP가 +면 E=X+Y의 형식을 계산해주기 위한 매크로이다.
다만 조건에서 정수형끼리의 계산에는 정수형으로 출력할 필요가 있었다. 이를 조건문을 통해 해결을 하였다.
위와 비슷한 구조로 다음과 같은 매크로들을 작성했다.
- SINGLE_ARITH
- SINGLE_ARITH2
- POW
- Memory_save
- Memory_load
- CAST
SINGLE_ARITH의 경우에는 형태를 신경쓰지않고 OP(X)구조의 연산을 진행한다.
log나 cos이다 exp의 함수에 정수값을 입력했다고 정수부분만 반환하는 것은 누구도 원하지 않을 것이라고 생각한다.
반면 SINGLE_ARITH2는 변수형을 고려하여 OP(X)의 연산을 진행한다
절댓값의 계산이나 부호반전을 위해 사용된다.
POW는 사실 OP(X,Y)의 연산을 위해 사용되어질 수 있다. 하지만 문제의 스펙상 이 기능은 pow에밖에 쓰지 않아서 다음과 같은 이름으로 정의했다. 전체적 구조는 ARITH와 같으나 X OP Y가아닌 OP(X,Y)로 결과가 들어간다.
메모리 역시 변수형을 기억할 필요가 있었다. 다음과 같은 구조로 메모리를 정의했다
#define M_SIZE 16
typedef struct{
char Type;
union {
int I;
double D;
} V_fld;
} M_struct;
M_struct Memory[M_SIZE];
먼저 메모리의 용량은 16개의 숫자를 저장할 수 있게 정의했다.
구조체는 변수의 구조체와 상당히 유사한 구조를 하고있다. 다만 그 구조체를 그대로 쓰면 변수의 정의가 충돌하여 위와같이 변수명을 돌려썼다.
메모리 매크로의 역할은 변수 정보를 메모리에 대입해주는 것과 메모리의 정보를 변수에 대입해주는 것이다.
/* Memoryに情報をセーブする*/
#define Memory_save(M, X) \
if (X.Type == INT) { \
M.Type = INT; \
M.V_fld.I = X.V_fld.I; \
} else {\
M.Type = DBL; \
M.V_fld.D = X.V_fld.D; \
}
/* Memoryの情報をロードする*/
#define Memory_load(X, M) \
if (M.Type == INT) { \
X.Type = INT; \
X.V_fld.I = M.V_fld.I; \
} else {\
X.Type = DBL; \
X.V_fld.D = M.V_fld.D; \
}
위와 같은 구조로 정의되어있다.
다음은 CAST매크로이다
#define CAST(R, T, X) \
if (T == INT && X.Type == DBL) { \
R.Type = INT; \
R.V_fld.I = X.V_fld.D; \
} else if (T == DBL && X.Type == INT){\
R.Type = DBL; \
R.V_fld.D = X.V_fld.I; \
} else {\
R=X; \
}
변수의 형변환을 해주는 코드이다. X를 T타입으로 변환하여 E에 저장한다.
다만 이미 같은 형에서의 변환의 경우에는 그대로 대입을 한다.
구문의 종류는 다음과 같이 3종류이다
- calc : 정상적으로 해석이 완료할 경우. 변수형에맞춰 출력하며 계산중 오류 발생시 에러를 출력한다
- expr : 필요한 수식들과 상수가 정의되어있는 곳으로 위에서 설명한 ‘변수’ 에 해당한다.
- mcell : 메모리를 관리하기 위한 구조로 M[x]라고 적으면 x번째 메모리에 대한 정보로 환원된다.
%type <ival> mcell
%type <Val> expr
mcell 은 결국 메모리중에서도 몇번째인지를 나타내는 정수가 중요하여 ival타입으로 정의하며
expr은 위에서 설명한 구조체인 Val로 정의되어진다.
그럼 실제로 간단한 해석 과정을 확인해보자
expr :
expr '+' expr { ARITH($$,$1,+,$3); }
| '(' expr ')' { $$ = $2; }
| INTC { $$.Type = INT; $$.V_fld.I = $1; }
다음과 같이 expr이 정의되어있을때 2+(3+2)에 대해 생각해보자
먼저 2는 INTC토큰으로 expr로 환원이 된다. expr(Type=INT V_fld.I =2)+(3+2)
가 된다.
그 옆을 보니 +가있다. 이 경우 문법상 해당되는 것은 없으나 그 뒤에 expr일 경우에 해당하는 경우가 존재하기에 +를 건너뛰고 (를 읽는다. 같은 원리로 ( expr ) 의 경우에 해석이 가능한 여지가 있으니 (도 건너뛰고 다음으로 간다.
숫자 3과 2는 앞의 2와 같은 원리로 INTC expr로 환원된다.
그럼 남은 것은 expr + ( expr + expr ) 이다.
expr + expr은 다시 expr로 환원될 수 있으며 이경우에 ARITH를 통해 다음 expr의 값들이 결정된다.
expr+(expr) 에서 (expr)은 다시 expr로 환원할 수 있다.
expr+expr 은 다시 expr로 환원이 된다.
이 결과는 다시 공규칙(空規則)인 calc로 넘어가 우리가 엔터를 눌러서 생긴 \n과 합쳐져 결과를 출력하고 구문해석이 성공한다.
이런 expr을 스펙에 맞게 줄줄이 써내려간다.
다만 문제가 하나 생겼다. 계산순서이다. expr의 짜임상 괄호내부는 무조건 따로 그 안에서 계산이 되게 되어져 있다. 하지만 4칙연산의 계산순서는 다르다. 이대로는 2+3*2 는 10이되어버린다.
또한 4칙연산뿐만이아니라 형 변환에도 문제가 생긴다 (INT)3.5+5.6는 8.6 (INT)(3.5+8.6)는 9여야한다 하지만 지금 이대로는 구별을 할 수가 없다. 이런 경우에 yacc를 컴파일하면 Warning이 나온다.
Warning: 10 shift/reduce conflicts [-Wconflicts-sr]
위와같은 에러가 나온다. conflicts는 충돌하는 문법이란 뜻으로 한가지 이상의 해석이 존재한다는 뜻이다.
이러한 해석 우선순위 문제는 다음과 같이 해결한다
%right '='
%left '+' '-'
%left '*' '/'
%right '^'
%left INT_CAST DBL_CAST
%right UMINUS
아래에 있을 수록 우선순위가 높으며 left right는 결합 방향을 나타낸다.
예를들면 ^가 right인 이유는 3^2+1을 생각해보자. left일 경우 ^는 3과 결합하여 3^ 상태로 뒤의 연산을 기다린다 즉 27이 나온다. 하지만 오른쪽일경우 3 ^2가되어서 9를 먼저계산해 10이라는 정상적인 결과가 나온다.
위와 같이 계산순서를 정의해주는 것으로 conflict를 제거하며 의도한 결과를 낼 수 있었다.
인코딩에는 bison과 flex가 필요하며 다음과 같이 인코딩했다
bison -dv -y ㅇ[filename].y
flex -l [filename].l
gcc y.tab.c lex.yy.c -lfl -lm -o NewCalc -w
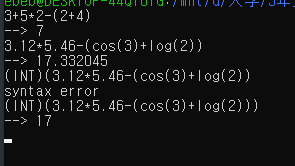위와 같은 느낌으로 잘 동작한다